Фильтрация данных в системах анализа и прогноза
Нет ничего практичней хорошей теории
К.Левин
О чем собственно речь?
Необходимость в фильтрации данных возникает каждый раз, когда нужно отделить передаваемое сообщение от искажающего его шума. Цель процесса фильтрации данных, а это могут быть не только результаты физических измерений, но и экономические показатели деятельности фирмы, и результаты социологических исследований, и т. д. – наилучшее восстановление первоначального сигнала на фоне помехи, или определение наличия полезного сигнала, или разрешение (различение) нескольких сигналов, присутствующих во входной последовательности.
Области приложения данной теории становятся все более и более многочисленными. Даже живая природа не обходится без обработки сигналов. Например, летучая мышь при ловле бабочек для определения местонахождения своих жертв использует лучшие из известных в настоящее время методы пространственной и временной селекции радиолокационных сигналов, они излучают ультразвуковой сигнал и соответствующим образом, фильтруя отраженный сигнал, определяют направление и расстояние до цели. Другой пример, наши органы чувств постоянно посылают в мозг огромное количество информации, и мы бы утонули в ее потоке, если бы не воспринимали только нужную информацию, иначе говоря – не фильтровали ее.
Логично предположить, что известные в настоящий момент методы обработки сигналов, широко применяемые при обработке результатов физических измерений (в радиолокации и радиотехнике), могут найти применение и при создании информационных систем анализа и прогнозирования.
Поиск взаимосвязи и закономерностей в анализируемых данных, при таком подходе, должен начинаться с того, что на соответствующем жаргоне называется первичная обработка данных. Это снизит остроту проблемы недостоверности данных, тем более, что полностью достоверных данных просто не существует, в любых данных присутствует шумовая составляющая, которую, по возможности, следует отфильтровать.
Последнее, о чем следует сказать. Цель этой статьи – способствовать практическому применению методов и алгоритмов обработки физических сигналов в системах анализа и прогноза, где имеют дело, в основном, с информацией другого рода.
К сожалению, общеизвестные работы, посвященные фильтрации данных, содержат несколько устрашающий математический аппарат, и это препятствует широкому распространению и использованию, которых заслуживает данная теория. Поэтому в данной статье хотелось бы математическим выводам придать прямое физическое истолкование, что позволяет интуитивно осмыслить ход математических рассуждений.
Итак, о каких методах обработки сигналов идет речь?
Введение в спектральный анализ
Разложение произвольной функции по заданной системе функций:
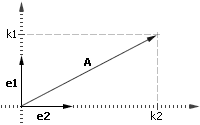
На рисунке 1 на плоскости заданы два ортонормированных вектора e1 и e2. Ортонормированные означает, что они ортогональны, то есть их скалярное произведение e1•e2=0 и длина их равна 1. Этого достаточно, чтобы любой вектор на этой плоскости можно было представить в виде A=k1•e1+k2•e2, то есть любой вектор можно представить в виде линейной комбинации некоторых базисных векторов. Коэффициенты к1 и к2 определяются как скалярное произведение вектора А на е1 и соответственно A на e2: k1=A•e1 и k2=A•e2. То же самое справедливо для любого n-мерного пространства.
Предыдущий абзац, по мысли автора, должен сделать более очевидными вещи, о которых речь пойдет ниже.
Бесконечная система функций (в общем случае комплексных) $\varphi_0(x), \varphi_1(x), \varphi_2(x),\dots \varphi_n(x), \dots$ называется ортогональной на отрезке $[a, b]$, если
$\int_{a}^{b}\varphi_n(x)\cdot \varphi_m(x)*dx=0 \mbox { при } n\neq m$ (1.1)
при этом: $\int_{a}^{b}\varphi_n(x)\cdot \varphi_n(x)*dx\neq 0$ (1.2)
Функция $\varphi_n(x)$, для которой
$\left \|\varphi_n(x)\right \|^{2} = \int_{a}^{b}\varphi_n(x)\cdot\varphi_n(x)*dx=1$ (1.3)
называется нормированной функцией, а система нормированных функций $\varphi_0(x), \varphi_1(x), \varphi_2(x),\dots \varphi_n(x), \dots$, в которой каждые две различные функции взаимно ортогональны, называется ортонормированной системой.
В математике доказывается (что и следовало ожидать после того, что изложено в первом абзаце этого раздела), что подавляющее большинство функций, определенных на интервале [a..b], могут быть представлены в виде суммы ряда:
$f(x)=c_0\varphi_0(x)+c_1\varphi_1(x)+c_2\varphi_2(x)+\cdot\cdot\cdot +c_n\varphi_n(x)+\cdot \cdot \cdot $ (1.4)
При этом, коэффициенты $c_n=\int_{a}^{b}f(x)\cdot \varphi_n(x)*dx$ (1.5)
Символ "звездочка" во всех этих формулах означает комплексно-сопряженную функцию.
Итак, подобно тому, как любой вектор можно разложить в некой системе координат, так и любую функцию можно представить в виде суммы некоторых базисных функций, взятых с соответствующими коэффициентами $c_0, c_1, c_2,\cdot \cdot \cdot, c_n, \cdot \cdot \cdot$
Коэффициенты, вычисляемые по формуле 1.5, есть коэффициенты Фурье, или преобразование Фурье, или спектр, а разложение 1.4 есть разложение в ряд Фурье.
Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении исходной функции в ряд. Это могут быть полиномы Чебышева, Эрмита, Лагерра, Лежандра и другие.
В радиотехнике наибольшее распространение получило разложение в базисе тригонометрических функций-синусов и косинусов, или, что то же самое, комплексных экспонент ejwt. И этому есть простое объяснение: гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении через любую линейную цепь. Изменяются лишь амплитуда и начальная фаза. Это очень удобно для анализа таких цепей.
Например, если мы каким-то образом определили, как данная линейная цепь пропускает через себя гармонические колебания разной частоты (например, рассчитали или измерили практически), то мы по сути знаем, как она будет реагировать на сигнал любой формы. Для этого надо:
- разложить этот сигнал на гармонические составляющие по формуле 1.5., то есть выполнить прямое преобразование Фурье (получим ряд комплексных чисел $c_0, c_1, c_2,\cdot \cdot \cdot, c_n, \cdot \cdot \cdot$ – или входной спектр).
- посмотреть, как каждая из этих составляющих изменится при прохождении через данную электрическую цепь (получим ряд комплексных чисел $c'_0, c'_1, c'_2,\cdot \cdot \cdot, c'_n, \cdot \cdot \cdot$, ... – или выходной спектр)
- и пользуясь формулой 1.4 получить выходную функцию времени. Процесс восстановления функции времени по ее спектру (то есть по коэффициентам $c'_0, c'_1, c'_2$ и т.д.) называется обратным преобразованием Фурье.
Другими словами, используется принцип суперпозиции (справедливый для линейных цепей), то есть реакция на сумму воздействий равна сумме реакций на каждое из воздействий. Этой нехитрой схемы рассуждений и будем придерживаться далее. Рассмотрим несколько примеров практического использования методов спектрального анализа.
Фильтр нижних частот
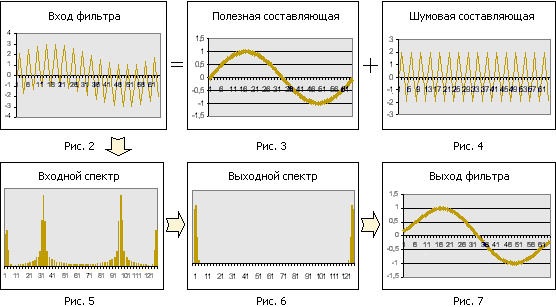
На вход фильтра поступает сигнал, изображенный на рисунке 2. Этот сигнал получен сложением двух синусоид разной частоты (рисунок 3 и 4), при этом частота помехи выше максимальной частоты, пропускаемой фильтром.
По формуле 1.5 получаем спектр входных данных (рисунок 5). Обнулив все составляющие, превышающие граничную частоту фильтра получаем выходной спектр (рисунок 6). По формуле 1.4 получаем выходной сигнал (рисунок 7).
Так как в качестве базисных функций выбраны функции ejwt и учитывая, что имеем дело с дискретными данными, формулы 1.5 и 1.4 будут выглядеть так:
$c_k=\sum_{n=0}^{N-1}x_n\cdot e^{-j2\pi kn/N}$ (1.6)
$x_n=\sum_{k=0}^{N-1}c_n\cdot e^{j2\pi kn/N}$ (1.7)
Здесь:
N – количество отсчетов во входных данных
$c_k$ – k-ая составляющая спектра
$x_n$ – n-ый элемент выходных данных.
Здесь реализован алгоритм фильтра нижних частот. То есть из всего многообразия гармонических составляющих входной последовательности отбираются лишь те, которые не превышают некоторую верхнюю частоту. Понятно, что таким же образом можно было выделить любую часть спектра, это был бы уже полосовой фильтр.
Именно так устроено человеческое ухо. Оно пропускает частоты от 20 Гц до 20 Кгц, и это очень кстати, так как иначе у нас в голове постоянно стоял бы страшный шум. (Это к вопросу о необходимости первичной обработки данных).
А как еще можно использовать фильтр нижних частот? Его можно использовать для сглаживания данных. Представим, что есть ряд данных, изображенный на рисунке 8.
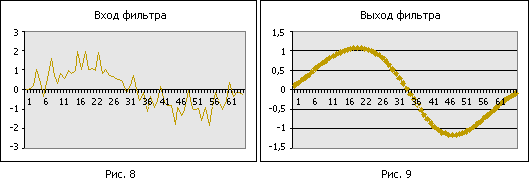
На выходе фильтра увидим что-то вроде изображенного на рисунке 9. Физический смысл этого прост. Есть сравнительно медленно меняющийся полезный сигнал и есть быстро флюктуирующая шумовая составляющая. Медленно меняющейся составляющей соответствует низкочастотная часть спектра, шуму – высокочастотные составляющие спектра. Отбрасывая последние, мы выделяем полезную составляющую.
Остается решить вопрос, какие частоты пропускать и какие отбрасывать. Было бы хорошо, если бы мы знали спектр полезного сигнала. В этом случае можно было не просто отбрасывать шумовые составляющие спектра, но и (чтобы еще больше уменьшить шум на выходе) полезные брать с соответствующими весами (дело в том, что полезный спектр и шумовой перекрываются).
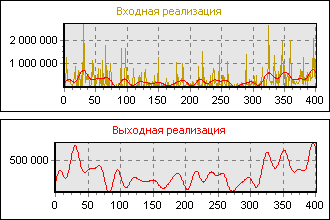
К сожалению, часто неизвестны не только параметры полезного сигнала, но и статистические свойства помехи. Остается надежда на здравый смысл, опыт и интуицию. На рисунке 10 изображены результаты фильтрации реальных данных. Вверху – до фильтра, внизу – после фильтра. Понятно, что выходные данные в большей степени поддаются прогнозированию, чем входные.
Кстати, о прогнозе. Предсказание поведения некоего процесса на заданный интервал времени возможно только тогда, когда его автокорреляционная функция достаточно медленно стремиться к нулю и для заданного интервала еще не достигла его. С другой стороны, автокорреляционная функция и квадрат модуля спектра процесса связаны тем же преобразованием Фурье, одно из свойств которого – чем шире спектр, тем быстрее изменение во времени, и наоборот, медленно меняющиеся во времени процессы имеют узкий спектр.
Вывод: прогноз тем точнее, чем уже спектр прогнозируемого процесса, и наоборот, всякий прогноз – неявное выделение низкочастотных составляющих исследуемого процесса, обужение спектра.
Оптимальная фильтрация
Было время, идеальным считался фильтр с П-образной характеристикой, то есть равномерное пропускание спектра полезного сигнала и полное подавление частот вне этого спектра. Такой фильтр мы и рассматривали выше. Если вы заметили, он никак не учитывает форму сигнала, которая может быть разной при одной и той же ширине спектра.
С развитием теории информации и статистической теории обнаружения сигналов эта трактовка существенно изменилась. И теперь, при наличии априорной (предварительной) информации о форме сигнала и статистических свойствах помехи, фильтр с П-образной характеристикой не является наилучшим. Несколько примеров. На рисунке 11 изображен исходный сигнал.
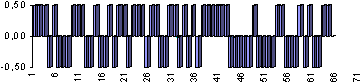
На рисунке 12 изображены исходный сигнал плюс тот же самый сигнал, сдвинутый на 1/8 его длительности и плюс равномерный шум.
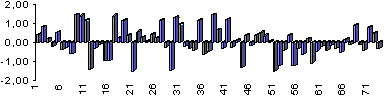
Как видно, картина сильно искажена. Тем не мене оптимальный фильтр уверенно отмечает наличие в этом хаосе двух сигналов (рисунок 13).
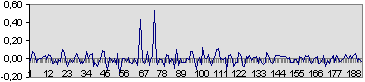
Дело в том, что данный фильтр является оптимальным по некоторому критерию именно для этого сигнала. А загадочная фраза об учете формы сигнала означает использование при фильтрации информации о фазе спектральных составляющих этого сигнала (если не совсем точно, фаза характеризует временной сдвиг каждой спектральной составляющей). Это позволяет оптимальному фильтру так сдвинуть по времени каждую составляющую полезного сигнала, что в определенный момент они сложатся в одной фазе, что мы и видим на рисунке 13.
Конечно, форма сигнала при этом теряется, но временное положение и его амплитуда измеряются с максимально возможной точностью. Возвращаясь к нашей предметной области, подобного рода алгоритмы могут быть применены для выявления скрытых тенденций в рассматриваемых данных. Эти закономерности замаскированы мешающим действием случайных факторов и тем обстоятельством, что обычно одновременно присутствуют несколько таких тенденций.
- К. Шеннон. Работы по теории информации и кибернетике. М. Иностранная литература, 1963
- И. С. Гоноровский. М. П. Демин. Радиотехнические цепи и сигналы. М. Радио и связь, 1994
- Ж. Макс. Методы и техника обработки сигналов при физических измерениях. М. Мир, 1983
- Ю. М. Коршунов. Математические основы кибернетики. М. Энергоатомиздат, 1987