Введение в RBF сети

Методология3 комментарияВерсия для печати

Радиально-симметричные функции

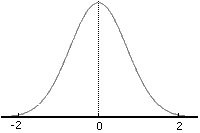
Радиально-симметричные функции – специальный класс функций. Их характерное свойство заключается в том, что отклик функции монотонно убывает (возрастает) с удалением от центральной точки. Типичный пример такой функции – функция Гаусса, для скалярного аргумента имеющая следующее аналитическое представление:

$h\,(x) = \exp\,\Bigl( -\,\frac{{(x\,-\,c)}^2}{r^2}\Bigr)$, (1)

Для случая c=0 и r=1 график функции изображен на рисунке 1.

Примером радиально-симметричных функций могут служить и другие функции:

$h\,(x) = {(x^2\,+\,\sigma^2)}^{-\alpha},\,\alpha\,>\,0$, (2)

$h\,(x) = \sqrt{(x^2\,+\,\sigma^2)}$, (3)

В случае векторной переменной х формулы не намного сложней; для функции Гаусса, например, формула приобретает вид:

$h\,(\overline{x}) = \exp\,\biggl( -\,\frac{{\| \overline{x}\,-\,\overline{c}\|}^2}{r^2}\biggr)$, (4)

Здесь и далее $\overline x$ обозначает вектор.

RBF сети

Радиально-симметричные функции – простейший класс функций. В принципе, они могут быть использованы в разных моделях (линейных и нелинейных) и в разных сетях (многослойных и однослойных). Традиционно термин RBF сети ассоциируется с радиально-симметричными функциями в однослойных сетях, имеющих структуру, представленную на рисунке 2.

То есть, каждый из n компонентов входного вектора подается на вход m базисных функций и их выходы линейно суммируются с весами: $\bigl \{w_j\bigr \}_{j=1}^m$

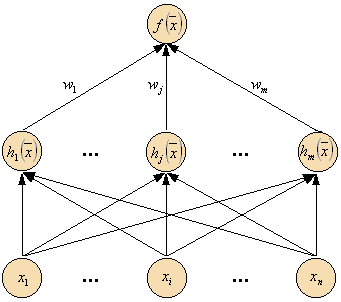
Таким образом, выход RBF сети является линейной комбинацией некоторого набора базисных функций:

$f\,(\overline{x}) = \sum_{j=1}^m \,w_j\,h_j\,(\overline{x})$, (5)

В дальнейшем под функцией h будем подразумевать функцию Гаусса с векторным аргументом вида 4.

Небольшое отступление

Вообще-то, никто не запрещает использовать в качестве базисных функций произвольный набор функций. Но использование в качестве таковых функций одного класса представляет особый интерес.

В математической статистике часто используют полиномиальные функции:

$$h_j\,(x) = x^j$$

Комбинация синусоидальных функций (ряды Фурье) часто используется при обработке сигналов:

$$h\,(x) = \sin\,\biggl( \frac{2\,\pi\,j\,(x\,-\,\theta_j)}{m}\biggr)$$

Логистические функции наиболее популярны в многослойных искусственных нейронных сетях:

$$h\,(x) = \frac{1}{1\,+\,\exp\,(bx\,-\,b_0)}$$

В любом случае речь идет об одном и том же: на основе некоторого набора экспериментальных данных типа "вход – выход" и в условиях полной неопределенности относительно формы возможной функциональной зависимости между входными и выходными данными пытаются угадать эту зависимость. В разных дисциплинах это называется по-разному: непараметрическая регрессия, аппроксимация функции, идентификация системы и т.д. В нейронных сетях это называется управляемое обучение или обучение с учителем. То есть каждый пример из обучающего множества содержит независимые переменные (входные) и соответствующие им зависимые переменные (выходные). При этом задача обучения сводится к тому, чтобы в соответствии с некоторым критерием оптимизировать параметры системы, осуществляющей искомое преобразование вход-выход. Таким критерием, в частности, может быть критерий минимума среднего квадрата ошибки на имеющемся обучающем множестве.

Давайте взглянем на проблему пошире. Классическое направление прикладной математики связано с методами вычислений одних характеристик изучаемого объекта по известным значениям других его характеристик. При этом модель объекта задана, а зависимости между характеристиками представлены аналитическими выражениями. Потом появились задачи анализа объектов, математическая модель которых известна с точностью до параметров, и в результате анализа экспериментальных данных в соответствии с некоторыми критериями выбираются значения этих параметров. Следующий этап – появление направления, именуемого задачами анализа данных, когда выбор модели и ее параметров производится путем проверки разных эмпирических гипотез и единственным источником информации для решения этих задач является таблица экспериментальных данных типа "вход-выход". Наконец, при решении задач анализа с использованием нейронных сетей вообще не предполагают использование какой либо модели изучаемого объекта. Все что в данном случае необходимо – конкретные факты поведения этой системы, содержащиеся в обучающем множестве. Тем не менее, одно простое, но фундаментальное предположение при этом все таки используется; это предположение о монотонности пространства решений, которое формулируется так: "Похожие входные ситуации приводят к похожим выходным реакциям системы" [1]. "При таком подходе мы не пытаемся познать систему так глубоко, чтобы уметь предсказывать ее реакцию на любые возможные внешние воздействия. Мы знаем лишь одно ее фундаментальное свойство: монотонность поведения в окрестностях имеющихся прецедентов. И этого обычно оказывается достаточно для получения практически приемлемых решений в каждом конкретном случае" [1].

Линейная модель

Но вернемся к настройке RBF сетей. Если предположить, что параметры функции 4, смещение с и радиус r фиксированы, то есть каким то образом уже определены, то задача нахождения весов в формуле 5 решается методами линейной алгебры. Этот метод называется методом псевдообратных матриц и он миними-зирует средний квадрат ошибки. Суть этого метод такова.

Находится интерполяционная матрица H:

$H =\begin{pmatrix} h_1\,(\overline{x}_1)&h_2\,(\overline{x}_1)&\cdots&h_m\,(\overline{x}_1)& \\ h_1\,(\overline{x}_2)&h_2\,(\overline{x}_2)&\cdots&h_m\,(\overline{x}_2)& \\ \vdots&\vdots&\ddots&\vdots &\\ h_1\,(\overline{x}_p)&h_2\,(\overline{x}_p)&\cdots&h_m\,(\overline{x}_p) \end{pmatrix}$, (6)

На следующем этапе вычисляется инверсия произведения матрицы H на транспонированную матрицу H:

$A^{-1} = {(H^T\,H)}^{-1}$, (7)

Окончательный результат, вектор весов рассчитывается по формуле 8:

$\overline{W} = A^{-1}\,H^T\,\overline y$, (8)

В приведенных обозначениях m – число нейронов в скрытом слое, p – размер обучающей выборки, а каждый вектор x состоит из n компонентов, где n – число входов сети.

Все, что для этого необходимо – умение умножать, транспонировать и инвертировать матрицы.

Нелинейная модель

Если предыдущее предположение о фиксированных параметрах функции активации 4 не выполняется, то есть помимо весов необходимо настроить параметры активационной функции каждого нейрона (смещение функции и ее радиус), задача становится нелинейной. И решать ее приходится с использованием итеративных численных методов оптимизации, например, градиентных методов. В последнее время получили распространение методы обучения RBF сети, в которых используется сочетание генетических алгоритмов для подбора параметров активационных функций и методов линейной алгебры для расчета весовых коэффициентов выходного слоя по формуле 8. То есть на каждой итерации поиска генетический алгоритм самостоятельно выбирает в каких точках пространства входных сигналов сети разместить центры активационных функций нейронов скрытого слоя и назначает для каждой из них ширину окна. Для полученной таким образом совокупности параметров скрытого слоя по формуле 8 вычисляются веса выходного слоя и получающаяся при этом ошибка аппроксимации, которая служит для генетического алгоритма индикатором того, насколько плох или хорош данный вариант. На следующей итерации генетический вариант отбросит плохие варианты и будет работать с наборами, показавшими наилучшие результаты на предыдущей итерации. Алгоритм этой процедуры представлен на рисунке 3.

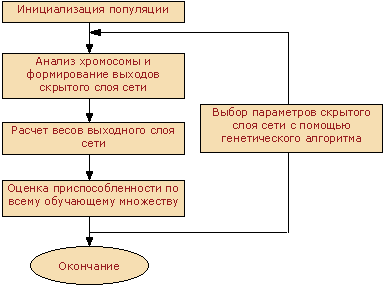
Статью о том, как работает генетический алгоритм и его программную реализацию можно найти на этом сайте.

Эту благостную картину омрачает лишь одно обстоятельство: как выбрать количество нейронов в скрытом слое. По большому счету, проблему можно было бы решить просто: число нейронов в скрытом слое сделать равным числу входных шаблонов в обучающем множестве, совместить центр каждой активационной функции с одним из шаблонов обучающего множества и задать такие их радиусы, чтобы они не перекрывались. При этом обучение как таковое будет отсутствовать, потребуется просто рассчитать веса выходного слоя по формуле 8. Но что делать, если размер обучающего множества 1000 или 10000 шаблонов? Работать с такой сетью невозможно, да и работать с матрицами таких размерностей на этапе обучения тоже нереально. Очевидный выход из этого тупика – сгруппировать шаблоны обучающего множества по степени их близости в пространстве входных значений в меньшее число кластеров. Количество таких кластеров задает количество нейронов в скрытом слое сети, а их средние характеристики используют для начальной инициализации параметров активационных функций: смещение и радиус. Для такого рода группировки(другие возможные термины: автоматическая классификация, самообучение, кластеризация) можно использовать в простейшем случае метод k-средних, самоорганизующиеся карты Кохонена или деревья решений. Все эти технологии представлены на нашем сайте, начиная от описания математического аппарата и заканчивая их программной реализацией.

Этот смешанный алгоритм обучения RBF сети сходится гораздо быстрее, чем алгоритм обратного распространения для обучения многослойных перцептронов. Однако RBF сеть часто должна содержать слишком большое число скрытых элементов. Это влечет более медленное функционирование RBF сети, чем многослойного перцептрона.